What is the 2x2 matrix that is a reflection across the line y= 2x? For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflectionThis lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitter

Linear Algebra Reflection In Any Linear Line Y Ax B Youtube
How to reflect over the line y=x
How to reflect over the line y=x-The ycoordinate changes, xcoordinate remains Reflecting across the line y = x;Reflection about the line y = x Reflecting over Any Line When we look at the above figure, it is very clear that each point of a reflected image A'B'C' is at the same distance from the line of reflection as the corresponding point of the original figure In other words, the line x = 2 (line of reflection) lies directly in the middle




Sketch The Graph Of The Function And Check The Graph Chegg Com
90˚ counterclockwise rotation about the origin OR 270˚ clockwise rotation about the origin Which rigid motion maps A(3, 1) to A'(3, 1)?Reflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =Reflecting across the line x = k (k is a constant);
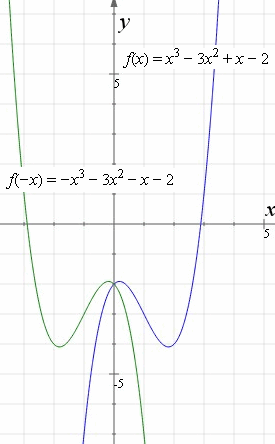
When you reflect a point across the line y = x, the xcoordinate and ycoordinate change places If you reflect over the line y = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed) the line y = x is the point (y, x) the line y = x is the point (y, x)Free functions symmetry calculator find whether the function is symmetric about xaxis, yaxis or origin stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyOn a coordinate plane, triangle A is reflected across the xaxis to form triangle B Triangle A is rotated to form triangle C Triangle B is a reflection of triangle A across the xaxis Triangle C is not a reflection of triangle A Triangle B is a reflection of triangle A across the yaxis Triangle C is a reflection
A reflection can occur across any line, it is not limited to the three lines discussed previously The example below demonstrates a reflection that is not specific to the axes or the line y = x Examine the drawing below to see the relationship between theIn this video, you will learn how to do a reflection over the line y = x The line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 For triangle ABC with coordinate points A (3,3), B (2,1), and C (6,2), apply a reflection over the lineThe xcoordinate changes, ycoordinate remains Reflecting across the line y = k (k is a constant);




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Solved Sketch The Graph Of The Function And Check The Graph With A Graphing Calculator Before Doing So Describe How The Graph Of The Function Ca Course Hero
If (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed;Math geometry 3 people liked this ShowMe Flag ShowMe Viewed after searching for reflect over x= 1 reflection over the line y=x Reflection over y=x reflection over yaxis Answers 3 on a question Which statement correctly describes the diagram?



Point Reflections Formula And Examples Explained With Applet Examples And Practice Problems Center At Origin And At Any Arbitrary Point



How To Reflect A Graph Through The X Axis Y Axis Or Origin
The line that represents y=x has a slope of 1/1 If i am considering a point, ill refer to it as A at (4,3) and reflect it over line y=x i will be at (4,3) which i will refer to as point B I can prove this relationship using simple geometry I wi1 an instance of reflecting especially the return of light or sound waves from a surface 2 the production of an image by or as if by a mirror 3a the action of bending or folding back180˚ rotation about the origin (clockwise or counterclockwise would give you the same result)




Reflection Mathbitsnotebook A1 Ccss Math




Algebraic Representations Of Reflections
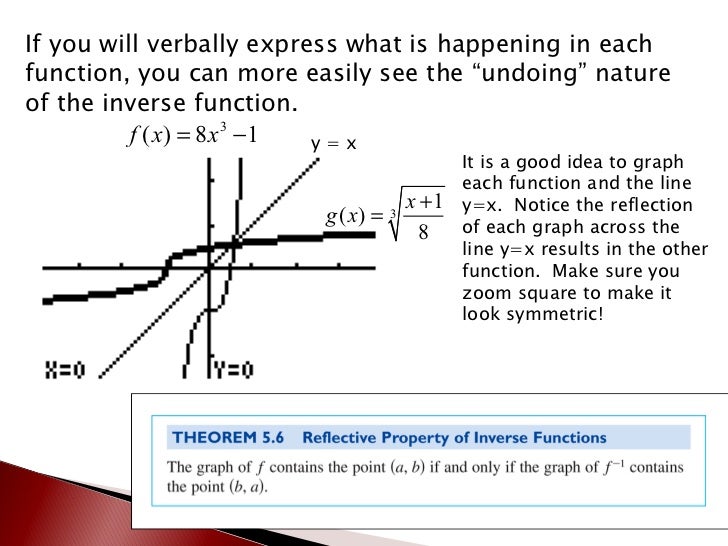
First you have to get the perpendicular s(x) = ms ⋅x t s ( x) = m s ⋅ x t (the dashed red line) You have to know this ms = − 1 m m s = − 1 m And then you know that P P is on s s So you simply put in the values x,y x, y of P and solve to t t t = y−ms ⋅x t = y − m s ⋅ x Now you have s s As s s and g g have exactly pointFinding the inverse from a graph Your textbook probably went on at length about how the inverse is "a reflection in the line y = x"What it was trying to say was that you could take your function, draw the line y = x (which is the bottomleft to topright diagonal), put a twosided mirror on this line, and you could "see" the inverse reflected in the mirrorFor a reflection in the line y=x $$\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$$ Example We want to create a reflection of the vector in the xaxis $$\overrightarrow{A}=\begin{bmatrix} 1 & 3\\ 2 & 2 \end{bmatrix}$$ In order to create our reflection we must multiply it with correct reflection




Reflection Transformation Matrix




21 T Math Geo T1 Cbt Section 1 No Calculator Section Question 1 4 Based On The Graph Brainly Com
Reflect over XAxis Example How to reflect over the xaxis?The equation of the line of the mirror line To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1A reflection in a line produces a mirror image in which corresponding points on the original shape are always the same distance from the mirror line The reflected image has the same size as the original figure, but with a reverse orientation



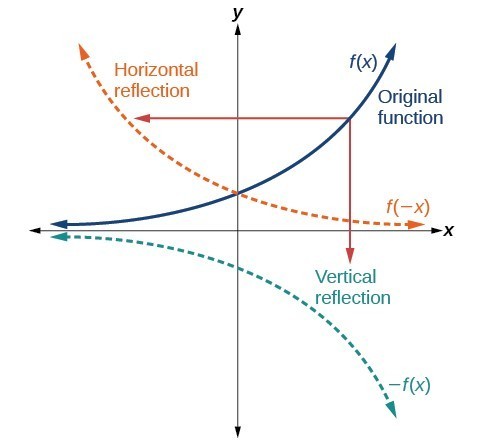
Transformations Of Functions College Algebra



5 Filtering Data Paraview Documentation 5 8 1 Documentation
Then reflect the graph across the line y=x to obtain the graph of its inverse y=5x8 Expert Answer 100% (1 rating) Previous question Next question Get more help from Chegg Solve it with our algebra problem solver and calculator A reflection maps every point of a figure to an image across a fixed line What does reflection mean in English?Explain how you know What is the domain?




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
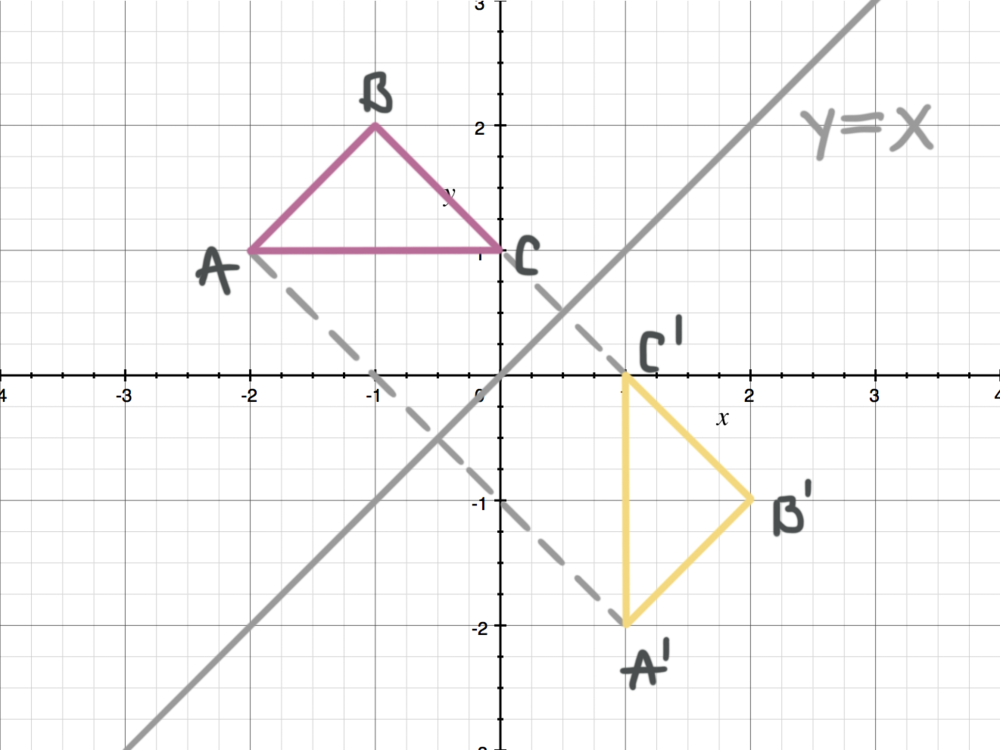



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
Reflection, Geometric Transformations Click and drag the blue dot to see it's reflection across the line y=x (the green dot) Pay attention to the coordinatesReflection across the xaxis givesReflections A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection



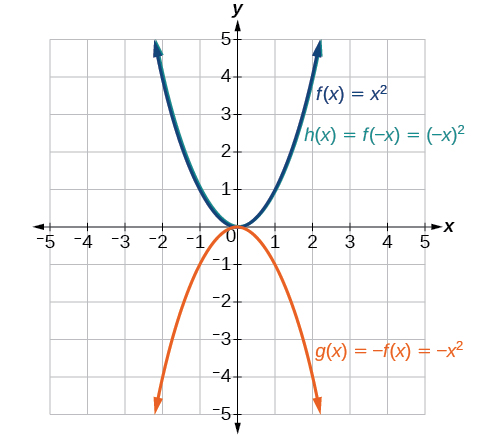
Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




Reflection Transformation Matrix
Expert Answer Previous question Next question Get more help from Chegg Solve it with our algebra problem solver and calculatorA reflection is a flip over a line You can try reflecting some shapes about different mirror lines here How Do I Do It Myself?Let's start from a picture that represents our reflection vector and the other vectors used in the calculation A representation of the



View Question Reflection Across The Line Y X



Desmos Accessibility
Reflection over Y = X When a point is reflected across the line y = x, the xcoordinates and ycoordinates change their place Similarly, when a point is reflected across the line y = x, the xcoordinates and ycoordinates change their place and are negated Therefore, The reflection of the point (x, y) across the line y = x is (y, x) TheReflection Translation of a quadrilateral across a line Notice that the lines extending from one point to its corresponding point are bisected by the line of reflection This means that to reflect a point, line, or object means to reconstruct it identical mirror image at exactly the same distance from the line/point of reflection Reflection can be found in two steps First translate (shift) everything down by b units, so the point becomes V=(x,yb) and the line becomes y=mxThen a vector inside the line is L=(1,m)Now calculate the reflection by the line through the origin,




Reflection In The Line Y X Geogebra




Reflection Transformation Matrix
The resulting orientation of the two figures are opposite The formula to calculate the reflection direction is R = 2 ( N ^ ⋅ L ^) N ^ − L ^ R = 2 ( {\hat {N}}\cdot {\hat {L}}) {\hat {N}} {\hat {L}} R = 2(N ^ ⋅L^)N ^ −L^ How is this formula obtained?Reflection over the line y = x Which rigid motion maps A(3, 1) to A'(1, 3)?
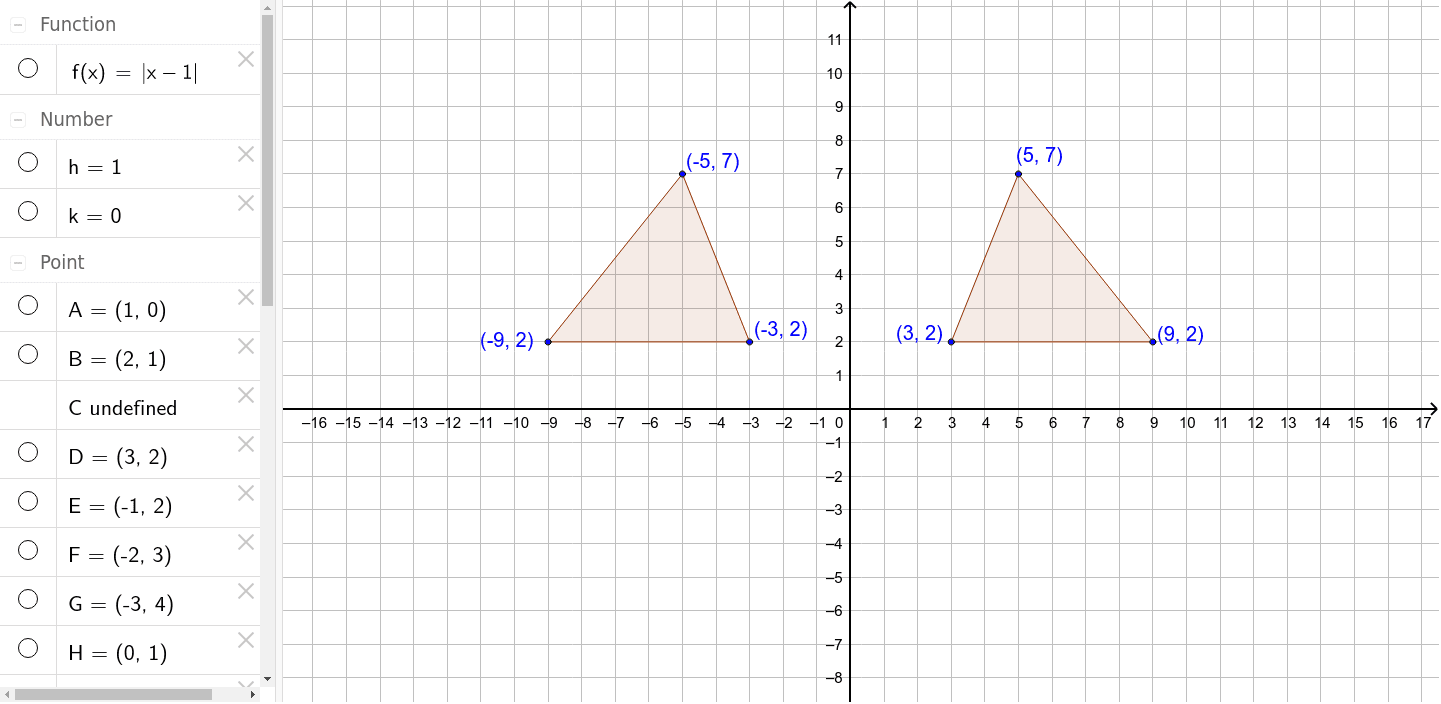



Reflection Over The Y Axis Geogebra




How To Find A Reflection Image
4 Fill in the table below for the new graph Best Answer #1 91 5 When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change places allthemmarvelfeels Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change size




A Couple Of Use Cases For Calc Css Tricks




Reflection Rules How To W 25 Step By Step Examples
Reflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC hasFirst, determine the original coordinate points For this example, we will say the coordinate points are (4,5) Next, calculate the new coordinate points Using the formula above we calculate the new reflected points as2 Answers2 Hint Reflections about the line y = x is accomplished by interchanging the x and the y coordinates Thus for y = f ( x), the reflection about the line y = x is accomplished by x = f ( y) For example, the reflection about the line y = x for y = x 2 is the equation x = y 2 Hope it helps




Hwq 1 12 15 Evaluate The Definite Integral No Calculator Please Ppt Video Online Download




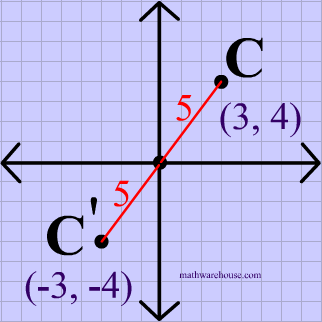
Learn About Reflection Over The Line Y X Caddell Prep Online
👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x13 Another way To reflect along a line that forms an angle θ with the horizontal axis is equivalent to rotate an angle − θ (to make the line horizontal) invert the y coordinate rotate θ back Further, y = mx implies tanθ = m, and 1 m2 = 1 cos2θ Then,Both the xcoordinate and the ycoordinate changes For any point, (x, y);
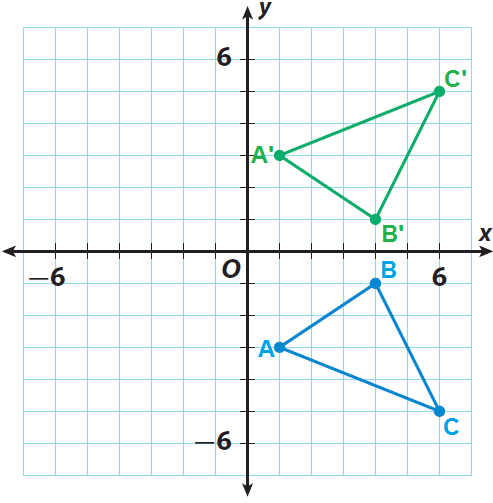



Algebraic Representations Of Reflections




Atan2 Wikipedia
Reflection Over Y=X Reflection Across Y=X When reflecting over the line y=x, we switch our x and y, and make both negative Reflection Over Y = X In order to define or describe a reflection, you need the equation of the line of reflection The four most common reflections are defined belowReflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $Reflection A shape can be reflected across a line of reflection to create an image The line of reflection is also called the mirror line The triangle PQR has been reflected in the mirror line
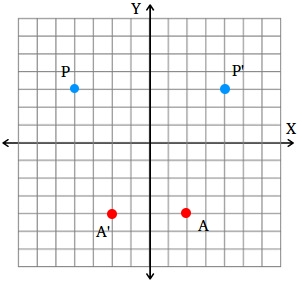



How To Find A Reflection Image




Reflection Over Y X Math Geometry Showme
Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)This calculator helps you to find the point reflection A, for the given coordinates of A (x,y) Just select an axis from the dropdown and enter the coordinates, the point reflection calculator will show the result Code to add this calci to your website Just copy and paste the below code to your webpage where you want to display this calculatorHere is an example of another kind of reflection that will frequently arise in our discussion of functions 1 What happens when we replace our xvalue with our y
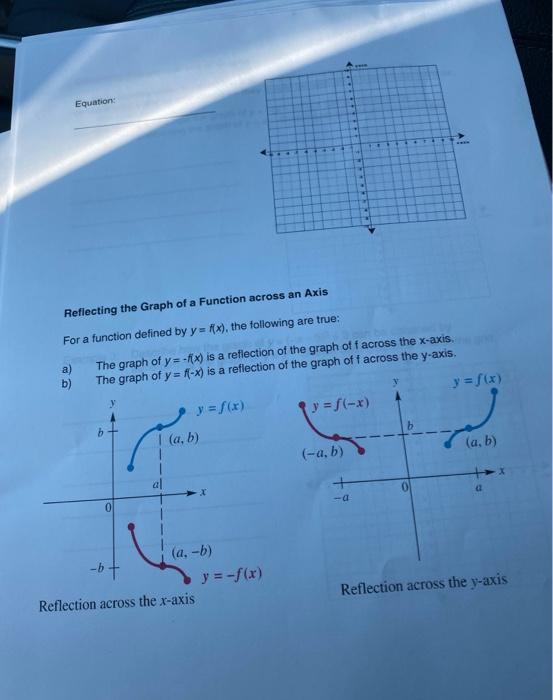



Solved Name Section 2 3 Reflecting Graphs Reflecting Acr Chegg Com




Answered Sketch The Graph Of The Function And Bartleby
B Reflection of a figure across a line 6 Click on the button "0, 1 or 2 reflections" in order to have 1 reflection To generate a figure such as a triangle, rectangle or an even more complicated figures, click anywhere on the plot screen to plot connected points and adjust the position of these points by dragging themThis is a KS3 lesson on reflecting a shape in the line y = −x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = −x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendableWhat is the range?




Calculating Grease Quantity Frequency



Transformation Reflection Over X Axis
Moreover, how do you calculate reflection?Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyTo label the axes Reflect the graph of f(x) across the line y = x by holding the topright and bottom left corners of the patty paper in each hand and flipping the sheet of patty paper over Sketch what you see Is this new graph a function?
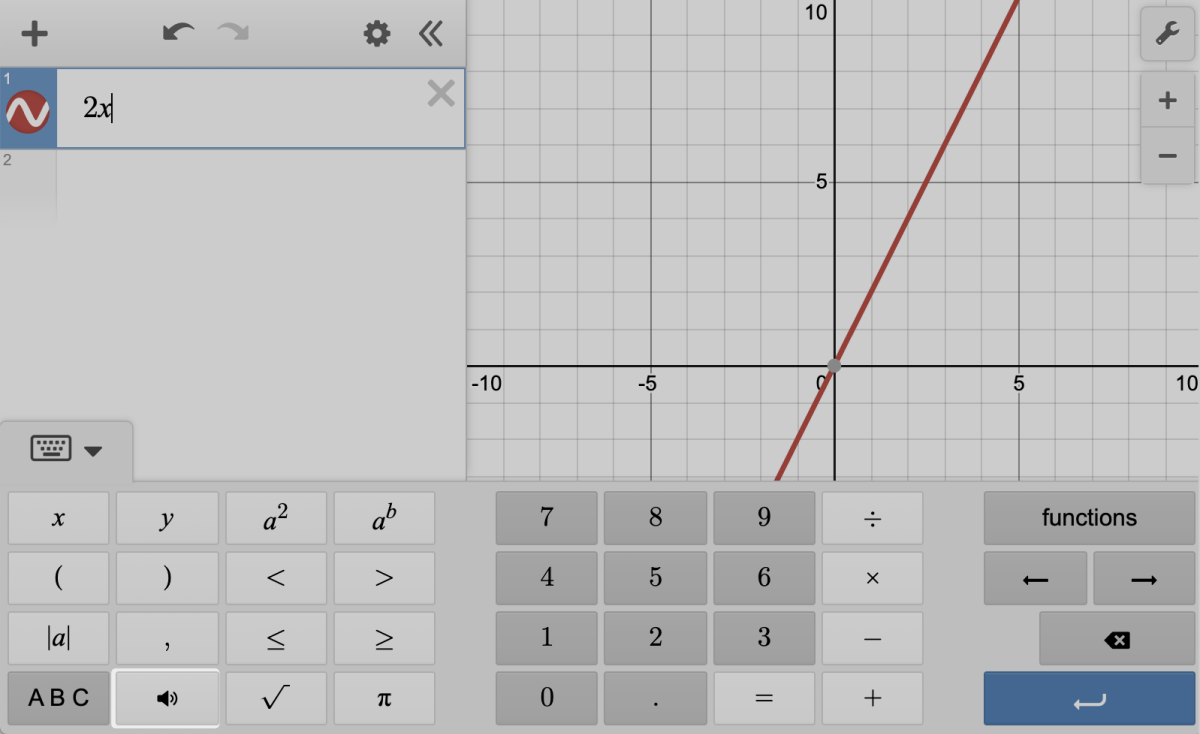



Desmos Accessibility



5 Filtering Data Paraview Documentation 5 8 1 Documentation
The linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (mPoints reflected across x axis Loading Points reflected across x axis Points reflected across x axis Log InorSign Up − 7, − 6 1 − Calculus Tangent Line example Calculus Taylor Expansion of sin(x) example Calculus Integrals example Calculus Integral with adjustable bounds x = 4 is a vertical line so the reflection will involve a horizontal move keeping the same distance from x = 4 but on the opposite side The y coordinate will stay the same As (3, 2) is one unit to the right of the line the point will move to




Grow Light Efficiency Calculation Tool Ppfd Watt Compared For All Grow Light Systems



Q Tbn And9gctvjthqkdwbpqfxmfukfqyrhm8wtlbtfnfu2u0osqggs0pct8ms Usqp Cau
Just approach it stepbystep For each corner of the shape 1 Measure from the point to the mirror line (must hit the mirror line at a right angle) 2Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha



Sound Level Distance Damping Decibel Db Damping Calculation Calculator Change Distance Versus Sound Level Apps Reduction Drop Dissipation Spl Sound Transmission Loss Free Field Loss Sound And Distance Decrease Drop Fall




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
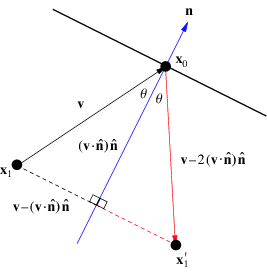



Reflection From Wolfram Mathworld
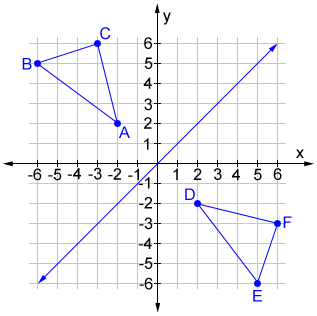



Reflection




Casio Fx 991ex Classwiz Non Programmable Scientific Calculator 552 Functions With Menu Driven Interface Amazon In Office Products




Linear Algebra Reflection In Any Linear Line Y Ax B Youtube



Wiki Documentfoundation Org Images 4 47 Cg41 Calcguidelo Pdf



Solved Reflecting Across The Y Axis To Set Up This Activi Chegg Com




Act Math Practice Question 11 Answer And Explanation Crackact Com




Vswr Return Loss Calculator Electrical Engineering Electronics Tools




Precalculus Notes Chapter 1



Calc 5 3




Reflection Rules How To W 25 Step By Step Examples




Hwq 1 12 15 Evaluate The Definite Integral No Calculator Please Ppt Video Online Download



Q Tbn And9gcqsn8 Oeiukut8na4ge1mme2jomkhd78afnf8gymhslwd7muyno Usqp Cau



1




Reflection Over The Y X Line Youtube




Calculator Wikipedia




Sketch The Graph Of The Function And Check The Graph Chegg Com




Reflection Over The Line Y X Geogebra




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



View Question Transformation



Reflect Over X Axis Calculator Calculator Academy



Point Reflections Formula And Examples Explained With Applet Examples And Practice Problems Center At Origin And At Any Arbitrary Point



Configuring The Layer Stack For Controlled Impedance Routing In Altium Designer Altium Designer 21 User Manual Documentation




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Basic Understandings Pdf Free Download




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation




Reflection Transformation Matrix




Reflection Rules How To W 25 Step By Step Examples



J3ido Naakcm



Warm Up You Should Be Able To Answer The Following Without The Use Of A Calculator 2 Graph The Following Function And State The Domain Range And Axis Ppt Download



Reflection Across A Line Geogebra




A Couple Of Use Cases For Calc Css Tricks




The Function F Defined By F X X2 Is Graphed In The Chegg Com




Reflection Transformation Matrix




Reflection Over The Line Y X Math Showme




Reflections Across Y X Geogebra



Graph Exponential Functions Using Transformations Math 1314 College Algebra
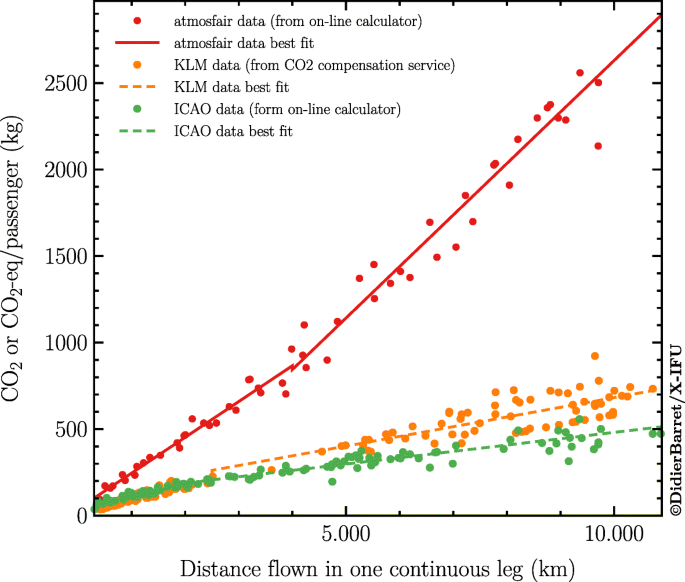



Estimating Monitoring And Minimizing The Travel Footprint Associated With The Development Of The Athena X Ray Integral Field Unit Springerlink
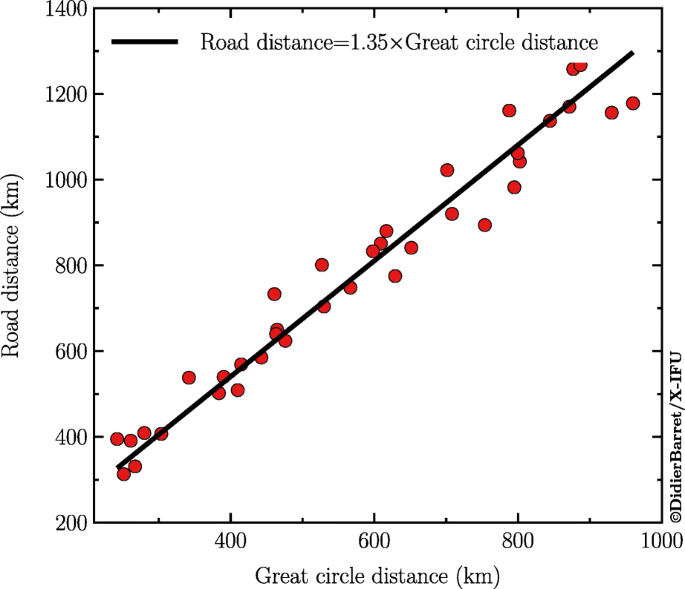



Estimating Monitoring And Minimizing The Travel Footprint Associated With The Development Of The Athena X Ray Integral Field Unit Springerlink
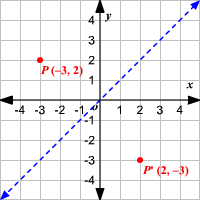



Reflections



1




Transformation Reflection Over The Line Y X Youtube



Documentation Libreoffice Org Assets Uploads Documentation En Cg7 0 Cg70 Calcguide Pdf
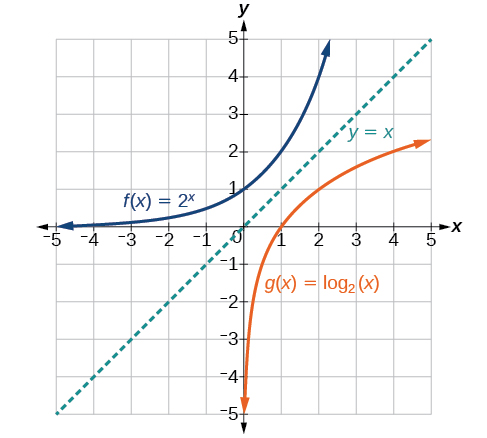



Graphs Of Logarithmic Functions Algebra And Trigonometry
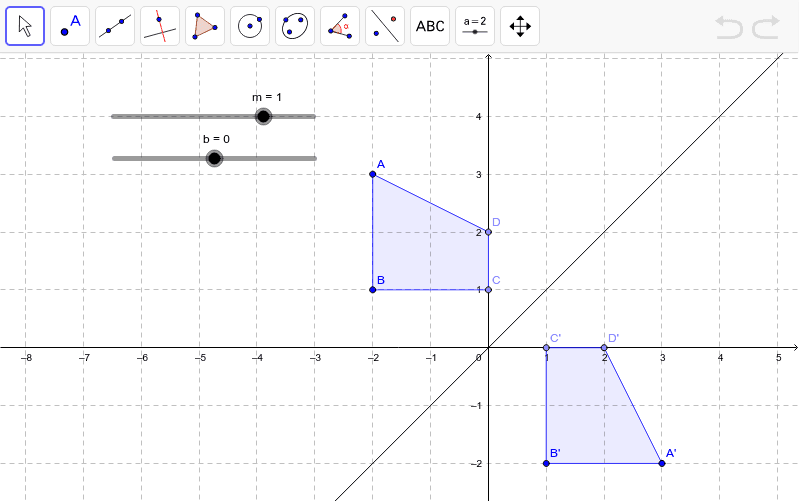



Reflection Over Y Mx B Geogebra



Kpis And Scorecard Calculation Complete Guide
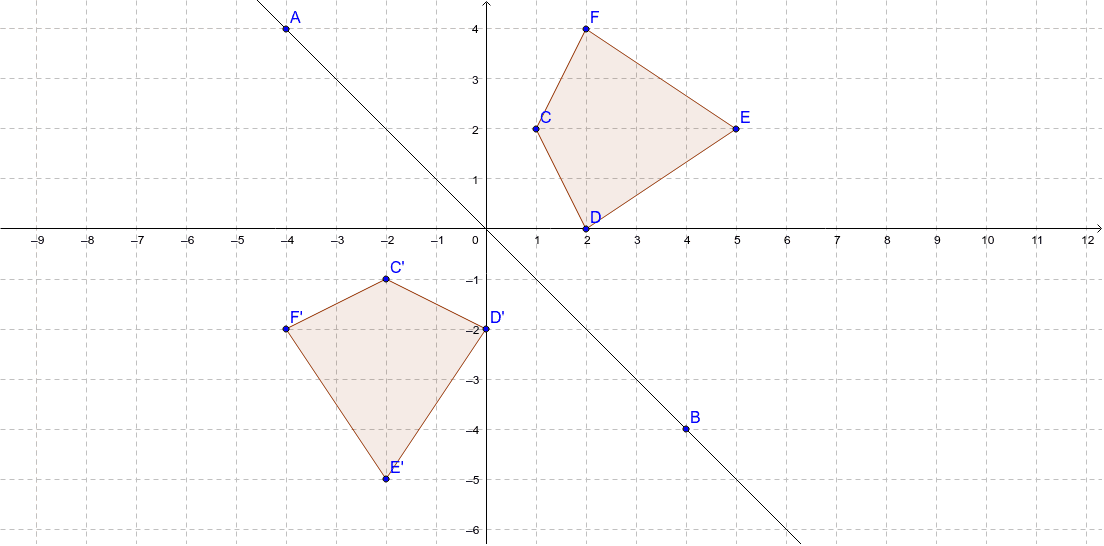



Reflection Over Y X Geogebra




Reflecting Functions Introduction Video Khan Academy
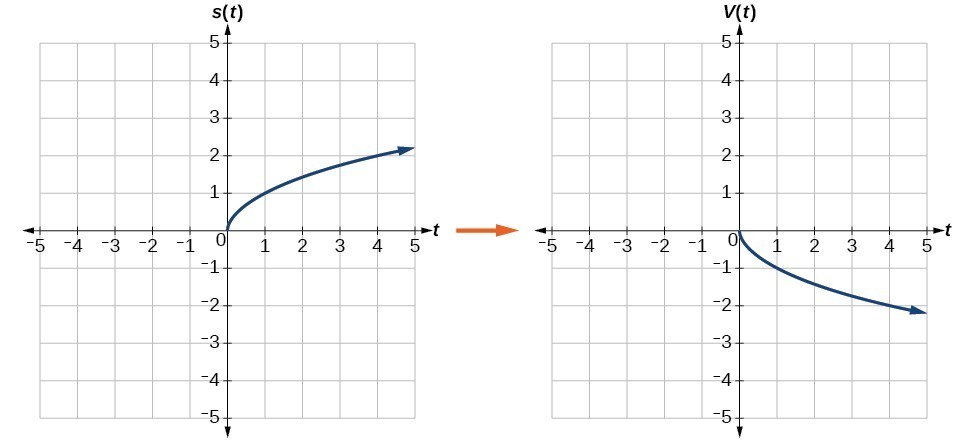



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
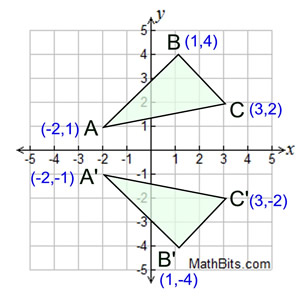



Reflection Mathbitsnotebook Geo Ccss Math



Rdi Calculator An Analysis Tool To Assess Rna Distributions In Cells Scientific Reports
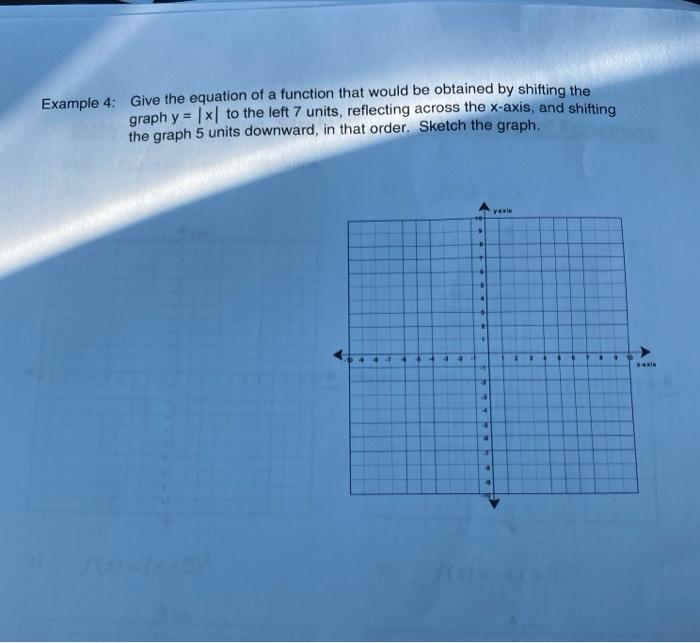



Solved Reflecting Across The Y Axis To Set Up This Activi Chegg Com




Erlang C Calculator Excel Including Shrinkage




Pin On Graphing Calculators
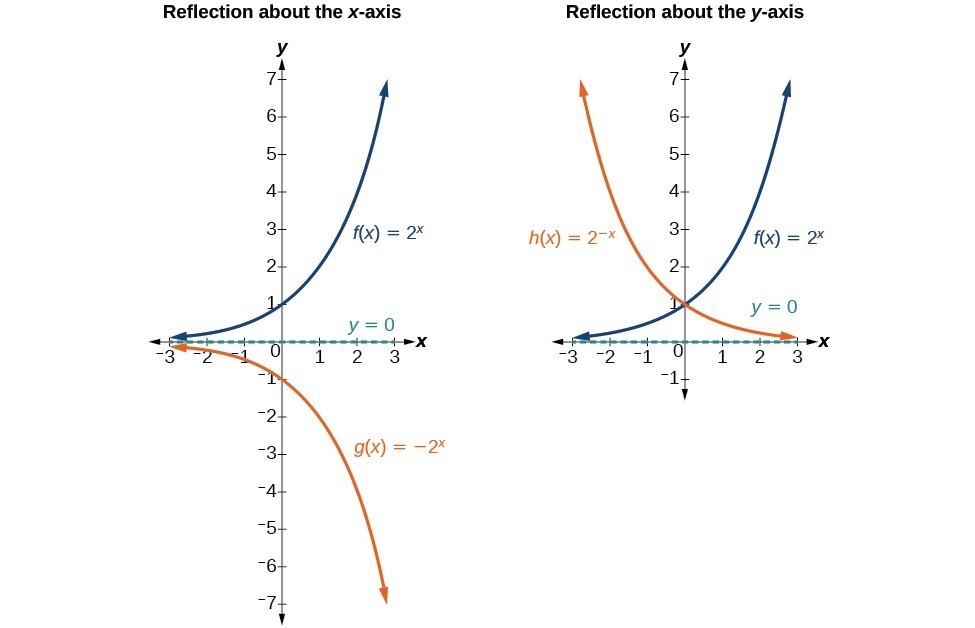



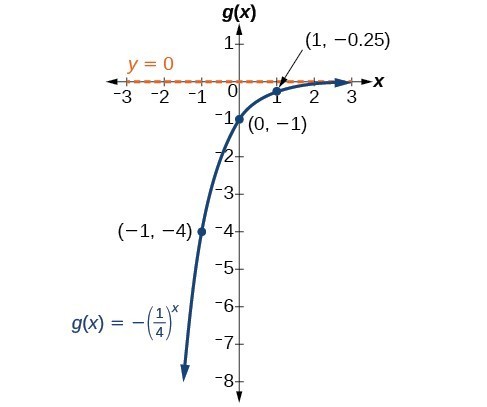
Graph Exponential Functions Using Transformations Math 1314 College Algebra




How To Find A Reflection Image



Transformation Reflection Over X Axis
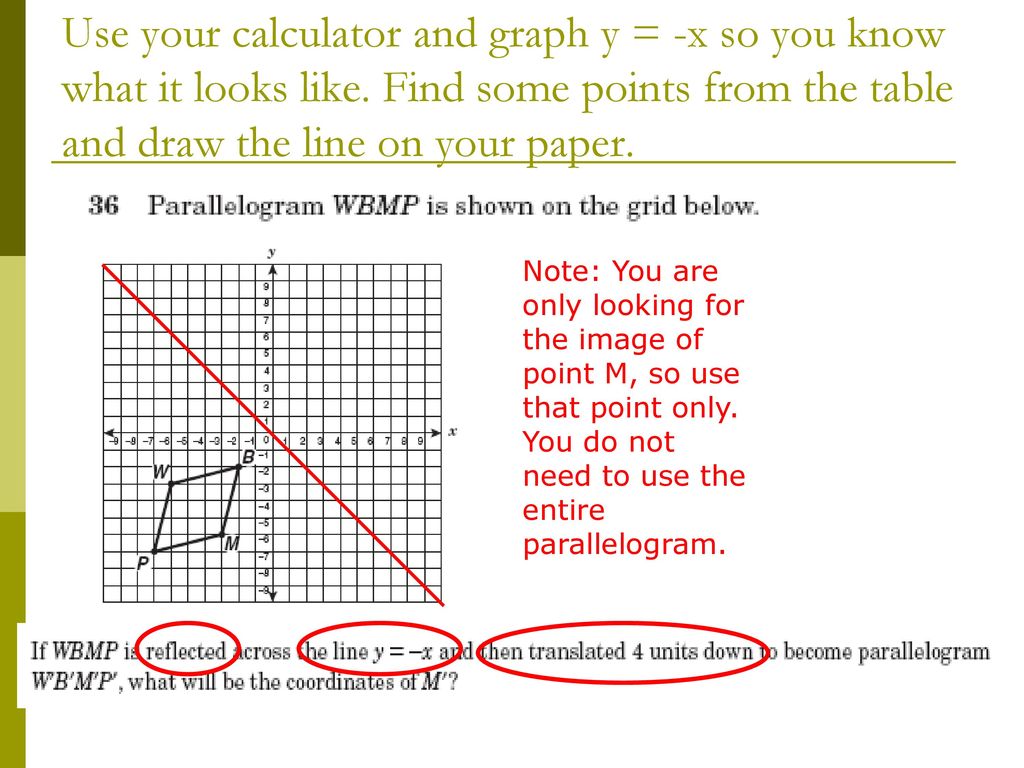



Geometry Objectives 6 8 Part 1 Ppt Download




Casio Fx ms 2nd Gen Non Programmable Scientific Calculator 240 Functions And 2 Line Display Amazon In Computers Accessories
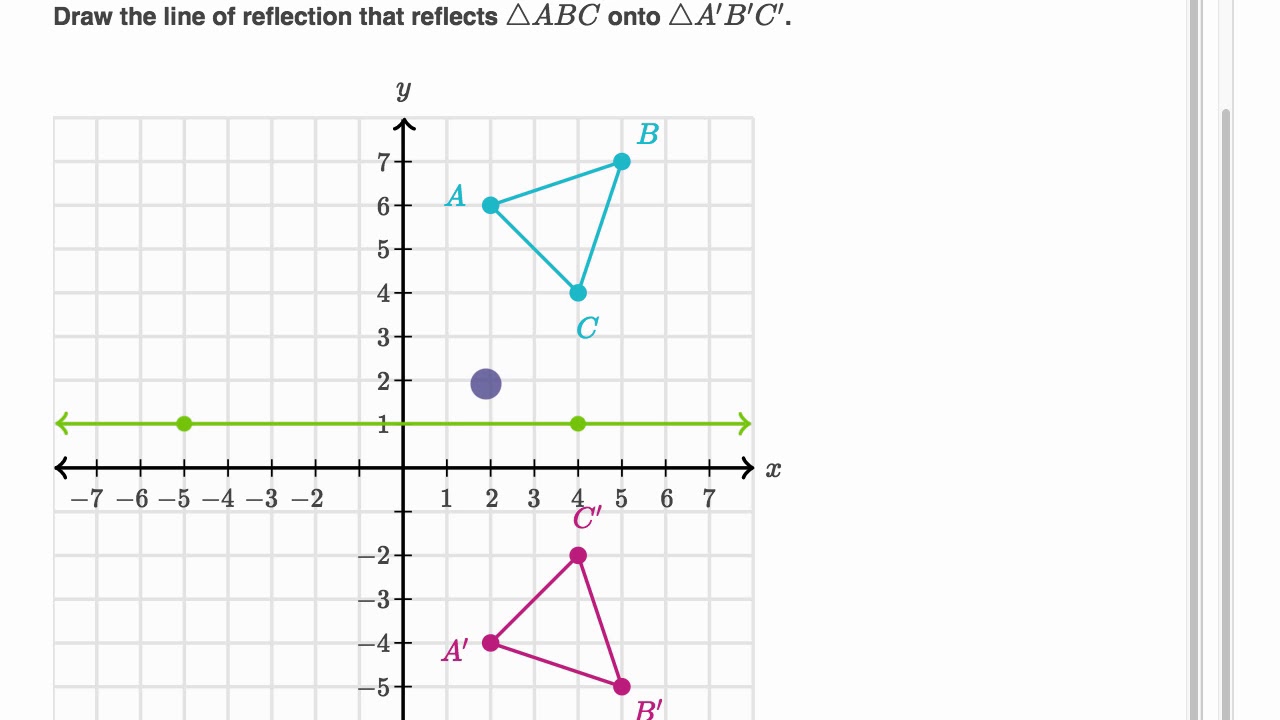



Line Of Reflection Example Youtube




Solved Consider The Function F X This Is A One To O Chegg Com



Creating A Chart Apache Openoffice Wiki
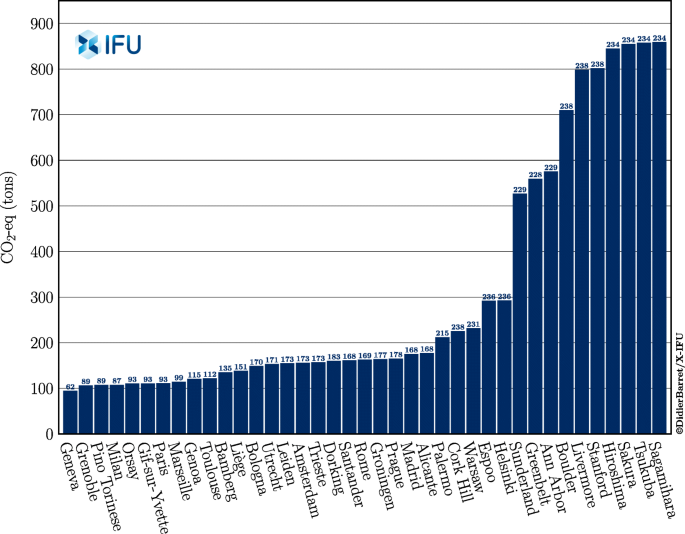



Estimating Monitoring And Minimizing The Travel Footprint Associated With The Development Of The Athena X Ray Integral Field Unit Springerlink
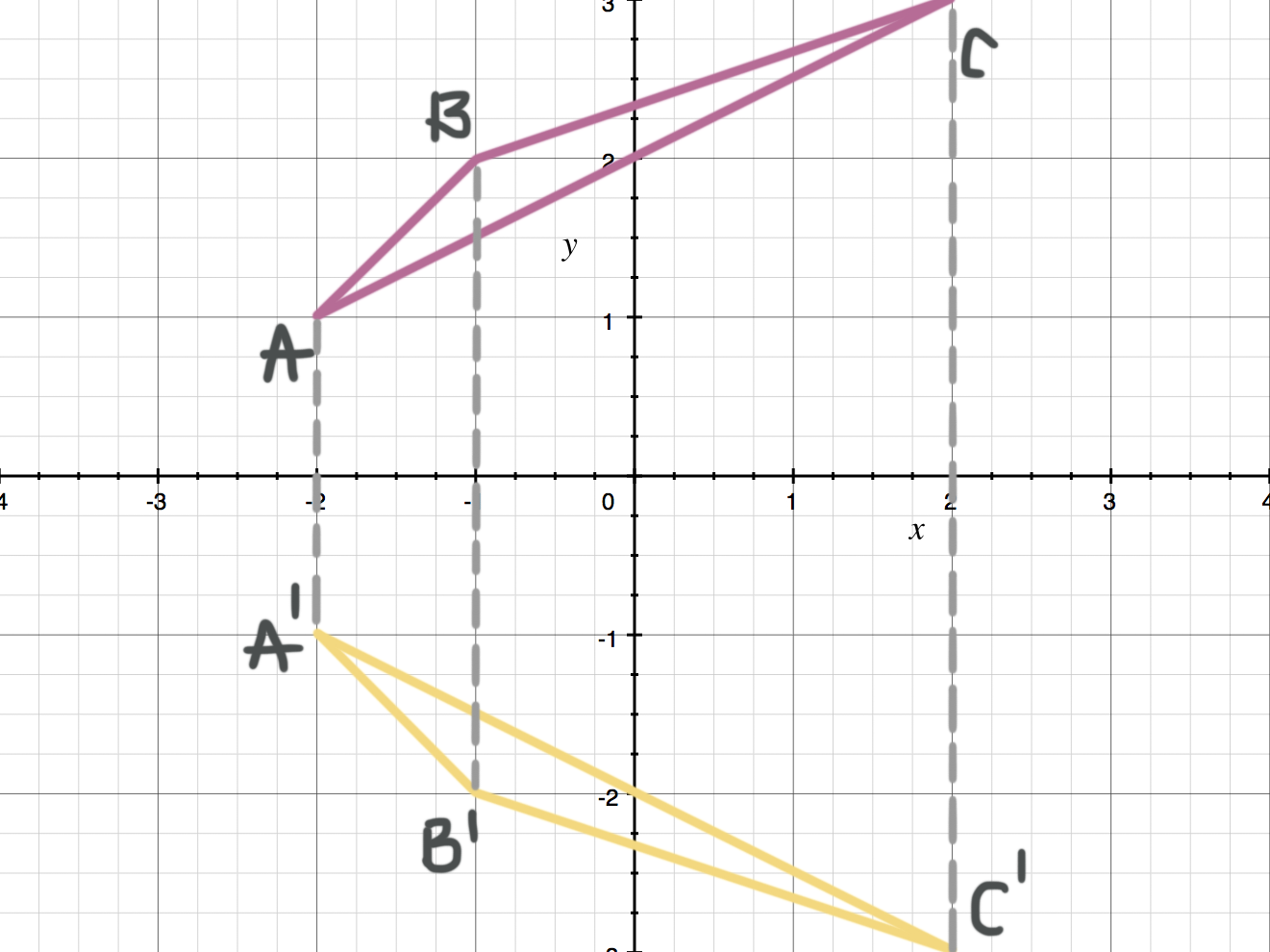



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
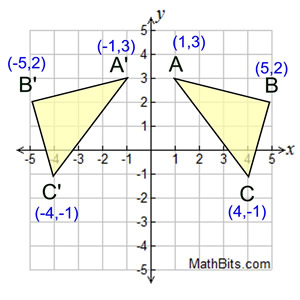



Reflection Mathbitsnotebook Geo Ccss Math



0 件のコメント:
コメントを投稿